Quantum #3 - Superdense Coding
This is the third post of a series of posts about Quantum Computing with Qiskit. The area is very new and the SDK is changing constantly, but hopefully, the series can help you learn a bit about quantum and help me reinforce a couple concepts.
The goal of this post is to discuss superdense coding, which can be seen as the opposite of quantum teleportation.
Sending bits with qubits
Imagine that Alice wants to send two classical bits \(b_{0}b_{1}\) to Bob. Alice could do that in more standard ways, but instead, Alice chooses to send a qubit to Bob. Is there a way we can guarantee that Bob will always decode \(b_{0}b_{1}\)? The answer is yes, and to communicate in such a non-standard way, Alice and Bob just need to follow an algorithm that is called Superdense Coding:
- Entangle Alice’s and Bob’s qubit
- Encode the bits Alice wants to send using quantum gates, and then send the qubit to Bob
- Apply the same gates from the entanglement procedure, but in inverted order
- Measure the two qubits
Notice that superdense coding can be seen as the opposite of teleportation. In teleportation, we share an entangled state and send two classical bits to recover a qubit. Superdense coding, on the other hand, uses an entangled state and sends a qubit to recover two classical bits. Thus, the processes are complementary.
Preparing the Bell state
The first step of the algorithm is to prepare the entangled state \(\vert\Phi^{+}\rangle\), one of the Bell states. We discussed that on the quantum teleportation, so if you want a detailed explanation I encourage you to check it out there. What we need to remember is that we work with the state:
\[ \vert\Phi^{+}\rangle = \frac{\vert 00 \rangle + \vert 11 \rangle}{\sqrt 2} \]
That is generated by the circuit:
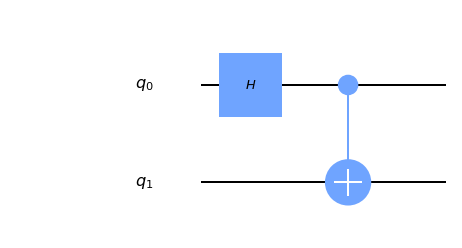
After generating \(\vert\Phi^{+}\rangle\), we send one of the qubits to Alice and the other one to Bob.
Encoding classical information on a qubit
Now that Alice has one of the qubits of \(\vert\Phi^{+}\rangle\), she can try to encode \(b_{0}b_{1}\) into the qubit by applying quantum gates.
To do so, she needs to find a clever way of applying a gate that after applying the inverted entanglement again, will give Bob the bits we were trying to send, i.e. the measurement of the first qubit will always be \(b_{0}\) and the second will always be \(b_{1}\).
To make it clearer, let’s take for example the \(|00\rangle\) case. We need to find a gate \(G\) such that:
\[ (H \otimes I)(CNOT)(G \otimes I)\vert\Phi^{+}\rangle = |00\rangle \]
We can then write the \(G\) matrix in the function of 4 unknown variables and recall that \(G G^{\dagger} = I\) to solve for \(G\). It turns out that for \(|00\rangle\), \(G = I\). That makes sense because applying the inverted entanglement circuit on the \(\vert\Phi^{+}\rangle\) untangles it.
We would need to do the same for \(|01\rangle\), \(|10\rangle\), and \(|11\rangle\). The table below summarizes the results we would get:
| \(b_{0}b_{1}\) | Gate to apply |
|---|---|
| \(00\) | \(I\) (no gates) |
| \(01\) | \(X\) |
| \(10\) | \(Z\) |
| \(11\) | \(X\) and then \(Z\) |
One curious connection to notice between quantum teleportation and superdense coding is that the table to apply the gates based on the bits is identical for both algorithms.
Decoding classical information from a qubit
After Alice is done encoding, she sends her qubit to Bob. Bob applies then the same gates we used to generate\(\vert\Phi^{+}\rangle\) but in inverted order. That is, we apply the CNOT gate and then Hadamard gate on the first qubit as in the circuit below:

Then, Bob measures the qubits. Because of the way we designed the gates in the last section, we are sure that the measurement of the first qubit will be \(b_{0}\) and the second will be \(b_{1}\). Hence, Bob has successfully received two bits of classical information! With just 1 qubit.
Verifying superdense coding computationally
We can verify that superdense coding works using Qiskit and running an experiment: in the Jupyter notebook below, we try the 4 different cases of bits that we can send.
Every step explained above is done, and the results match our prediction.