Quantum #2 - Teleportation
This is the second post of a series of posts about Quantum Computing with Qiskit. The area is very new and the SDK is changing constantly, but hopefully, the series can help you learn a bit about quantum and help me reinforce a couple concepts.
The goal of this post is to discuss quantum teleportation, one of the most basic protocols for communication in quantum computing.
Teleportation and the problem it solves
Imagine that Alice has a qubit \(| \psi \rangle = \alpha | 0 \rangle + \beta | 1 \rangle\), where both \(\alpha\) and \(\beta\) are unknown. Alice needs to send the qubit to Bob that is located somewhere far away. How does Alice do that?
One simple answer could be to measure \(\alpha\) and \(\beta\) and send the information. However, that does not work because:
- We may need an infinite amount of bits to represent \(\alpha\) and \(\beta\) (e.g. think about encoding \(\pi\) in binary, it has an infinite length)
- Every time we measure a qubit, it becomes either \(|0\rangle\) or \(|1\rangle\) and all its information is lost.
Having ruled out measurement, we may ask: is it even possible to send \(|\psi\rangle\)? The answer is, surprisingly, yes. To do so, we need two extra qubits, one for Alice and one for Bob, and to follow a simple algorithm:
- Entangle Alice’s and Bob’s qubit
- Apply a CNOT gate with \(|\psi\rangle\) as the control qubit and Alice’s qubit as the target
- Apply a Hadamard gate to \(|\psi\rangle\) and measure it, and measure Alice’s qubit
- Send the measurements to Bob through a classical communication channel
- Apply (or not) a \(X\) and/or \(Z\) gate based on the measurements
It may look like a lot to process at once, but if broken down, teleportation can make sense.
Preparing the Bell state
The first step of the algorithm is to prepare the entangled state \(\vert\Phi^{+}\rangle\), one of the Bell states. The Bell states are the most entangled and commonly appear in many quantum algorithms. Out of the for Bell states, the one we are looking is:
\[ \vert\Phi^{+}\rangle = \frac{\vert 00 \rangle + \vert 11 \rangle}{\sqrt 2} \]
To do so, we start with the two-qubit state \(\vert 00 \rangle\), and use a Hadamard gate on the first qubit.
\[ \vert 00 \rangle \rightarrow (\frac{\vert 0 \rangle + \vert 1 \rangle}{\sqrt 2}) \otimes \vert 0 \rangle = \frac{\vert 00 \rangle + \vert 10 \rangle}{\sqrt 2} \]
Notice that the state we are right now is very close to our goal. We just need to have \(|11\rangle\) instead of \(|10\rangle\), so we use a CNOT with the first qubit as control and second as the target. Nothing happens to \(|00\rangle\) because the control qubit is $|0$, but \(|10\rangle\) becomes \(|11\rangle\) because the control qubit is \(|1\rangle\). Overall:
\[ \vert 00 \rangle \rightarrow \frac{\vert 00 \rangle + \vert 10 \rangle}{\sqrt 2} \rightarrow \frac{\vert 00 \rangle + \vert 11 \rangle}{\sqrt 2} \]
The circuit that performs this step looks like:
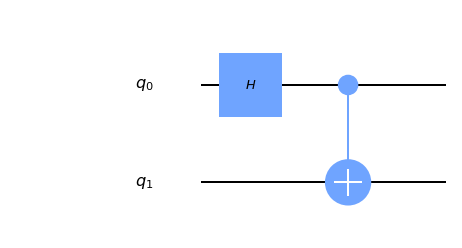
You may ask: how do we perform the entanglement if the qubits are far apart? That is indeed a good question. The first answer to this question would be to entangle the qubits when they are together with Alice and then split them apart, sending one to Bob. In my opinion, this answer violates the essence of teleportation: we do not want to send qubits to Bob.
The second answer is: assume we can do it at long distances. We have not been discussing the plausibility to have a qubit or apply the gates, so we will leave for physicists to figure out how to physically achieve the entanglement.
Teleportation procedure
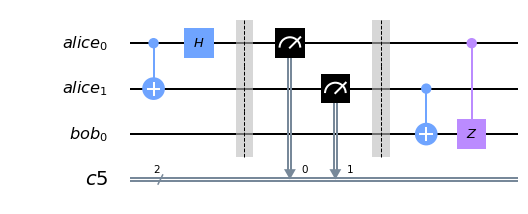
Now that we know how to generate \(|\Phi^{+}\rangle\), we have everything we need to do quantum teleportation. Considering our three-qubit system, we start with \(|\psi\rangle \otimes |\Phi^{+}\rangle\).
Firstly, we apply a CNOT gate with \(|\psi\rangle\) as the control, and Alice’s entangled qubit as the target. That yields:
\[ \frac{\alpha|000\rangle + \alpha|011\rangle + \beta|100\rangle + \beta|111\rangle}{\sqrt 2} \rightarrow \frac{\alpha|000\rangle + \alpha|011\rangle + \beta|110\rangle + \beta|101\rangle}{\sqrt 2} \]
Secondly, we apply the Hadamard gate to the first qubit and we obtain:
\[ \rightarrow \frac{|00\rangle (\alpha|0 \rangle+\beta|1\rangle) + |01\rangle (\alpha|1 \rangle+\beta|0\rangle) + |10\rangle (\alpha|0 \rangle-\beta|1\rangle) + |11\rangle (\alpha|1 \rangle-\beta|0\rangle)}{2} \]
Thirdly, we measure the first two qubits, i.e. those that are with Alice, and send the result to Bob. Notice that depending on the outcome, we know exactly the state of third qubit. For example, we know that if the outcome of the measurement is \(10\), then the last qubit is \(\alpha|0 \rangle-\beta|1\rangle\).
Lastly, we need to go from the qubit that we know now to \(|\psi\rangle\). Fortunately, that is simple. To achieve that, we need to apply the gates \(X\) and \(Z\) conditionally. The table below summarizes when we need to apply the gates:
| Outcome | Gate to apply |
|---|---|
| \(00\) | \(I\) (no gates) |
| \(01\) | \(X\) |
| \(10\) | \(Z\) |
| \(11\) | \(X\) and then \(Z\) |
Even though the math might have looked complicated, the final circuit is simple. The last part of applying gates conditionally can be done by applying a Controlled X gate (which is another name for CNOT), and also applying a Controlled Z gate. Hence, the circuit that performs all 4 steps is:
Verifying computationally that the procedure works
We can verify that quantum teleportation works using Qiskit and running an experiment: in the Jupyter notebook bellow, we try to teleport \(|\psi\rangle = \frac{\sqrt 3}{2}|0\rangle + \frac{1}{2}|1\rangle\) and analyse the results.
Every step explained above is done, and the results match our prediction.