Information Theory #3 - Broken Device

I am writing a series of posts about Information Theory problems. You may find the previous one here.

The problem we will analyze is Broken Device from the Japanese Olympiad in Informatics Spring Camp (JOI SC 2017). You may find the problem statement and a place to submit here.

A synthesis of the problem statement is : Anna wants to send a 60-bit integer to Bruno. She has a device that can send a sequence of 150 numbers that are either 0 or 1. The twist is that L (0 <= L <= 40) of the positions of the device are broken and can only send 0. Bruno receives the sequence Anna sent, but the does not know the broken positions. You must submit two files:

• One that given the integer X we want to send and the K broken positions, generates a sequence of length 150 that can be decoded.
• One that given the sequence generated by the previous procedure, decodes the integer X without knowing the K broken positions.

The subtasks are based on the maximum number of broken positions your algorithm can handle. Let's see some ideas for different K's.

K = 0 : 0 points

This is not a subtask, but you need to know how to solve this case in order to solve the full problem. The idea is very simple : send the binary encoding of X. We will use the binary encoding in all other subtasks , but you need to keep this idea in mind.

We use the first 60 positions to send the encoding and leave the other 90 unused.

K = 1 : 8 points

Because there is a broken place, we might not be able to send X using the 60 first positions. However, it will not be difficult to overcome that.

The key idea is to send a signal meaning that this is the place the binary representation starts. That is, the first number 1 of the sequence will mean “The following 60 numbers are the binary encoding of X”.

In order to use this idea, we need to be sure that there will 61 adjacent positions that are not broken. Because K = 1, we know that this is true.

K = 15 : 41 points

We will use a different strategy to send the binary encoding of X. The first step of our algorithm is to divide our 150 sequence into 75 buckets of size 2. The image bellow represents this idea , where grey is “0” and black is “1”.

This will allow us to use an encoding that is less affected by the broken places, because we will not need that a lot of adjacent non-broken positions.

Our encoding will use every 2 positions to send at most one bit. Notice that sometimes we may not send any information because of the broken places, but that is okay.

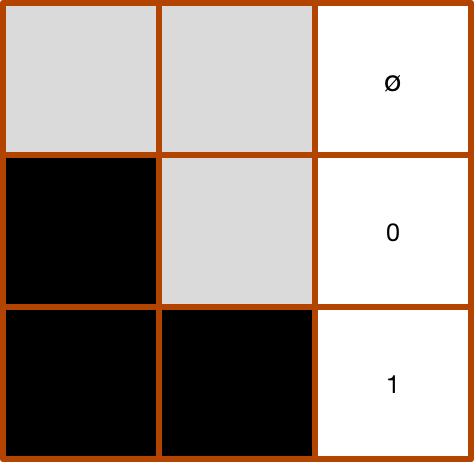
We will send the bits in order. If we receive “00”, then we did not send any information. If we receive “10”, this means that the next bit is “0”, and if we receive “11”, this means that the next bit is “1”.

By using this encoding , we can send up to 75 bits if there weren't any broken places. When there is at least one broken position in a bucket, in the worst case, we lose that bucket.

Considering we need to send 60 bits, we can afford to lose up to 15 buckets. So we solve to K up to 15.

Intermediary K's : 41+ points

We can improve the previous solution to handle more broken positions.

The first improvement is to find a meaning for “01”, something that we did not. By meaning we are not only talking about “1” or “0”, but other creative ideas like repeating previous numbers.

The second improvement is to use randomization in order to avoid the worst case of our algorithm:

• We may shuffle the position of the bits, in order to prevent the worst case where each broken position is on a different bucket
• We may change the integer we are sending by XORing it with a random number. This prevents cases where all numbers are 1 or 0, which can be bad for some ideas. To recover the original integer on the decoding part, we simply XOR the number we found with the random number

We need to carefully implement these ideas because we need to be able to revert the changes in the decoding part.

K = 40 : 100 points

The final solution is somewhat similar to the 41 points solution, but instead uses buckets of size 3.

With buckets of size 3 , we can create an encoding that sends up to 2 bits per bucket. Inefficient implementations of this idea do not score full points, but do better than the 41 point solution. I will go straight to the efficient implementation of the idea, but you may take sometime to create a encoding on your own.

Because of the size, we will use a encoding-table that is more resistant to broken places. The special property of the table is that it will allow us to send 2 bits of information in the case there are no broken places and 1 bit of information in the case there is one broken place.

Because of that, we can always send 60 bits regardless of the configuration. One possible table is the following :

My implementation of this idea: