Information Theory #2 - Navigation

I am writing a series of posts about Information Theory problems. You may find the previous one here.

The problem we will analyze is Navigation from the Japanese Olympiad in Informatics Spring Camp (JOI SC 2015). You may find the problem statement and a place to submit here.

A synthesis of the problem statement is : Anna lives in an island that is part of the IOI islands, that can be represented by an acyclic connected graph. Bruno will visit Anna, but he does not know the whole structure of the tree. He only knows the adjacent islands to the island he is currently at. To help Bruno , Anna will write an integer on each island such that Brunno can go to Anna's island using the short possible path.

We must submit two files:

• One that given the structure of the tree and the island Anna lives, writes a number on each island
• One that given the current island and its number, the adjacent islands to that island and their respective number, goes from that island to the one closest to Anna's island. In the case Bruno is already on Anna's island, you must not move.

The subtasks are based on the maximum number you wrote on the vertices of the tree.

Subtask 1 : No restrictions

For all subtasks , we will root the tree at Anna's island.

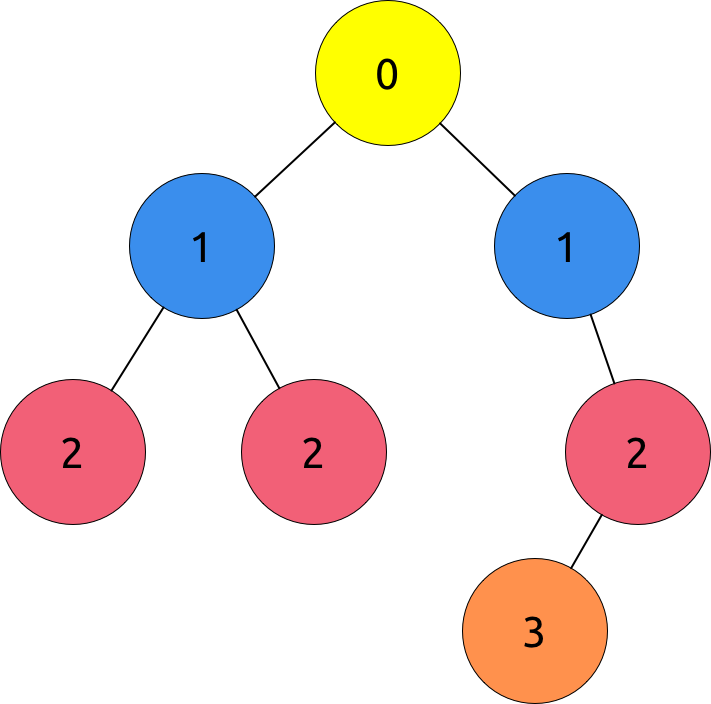
The idea for this subtask is to write on each node its distance from the root of the tree when we are encoding. The image above exemplifies this idea.

When we are decoding, we just go to the node whose number is the smallest.

Subtask 2 : use numbers 0, 1 and 2

We need to use something completely different from our previous solution.

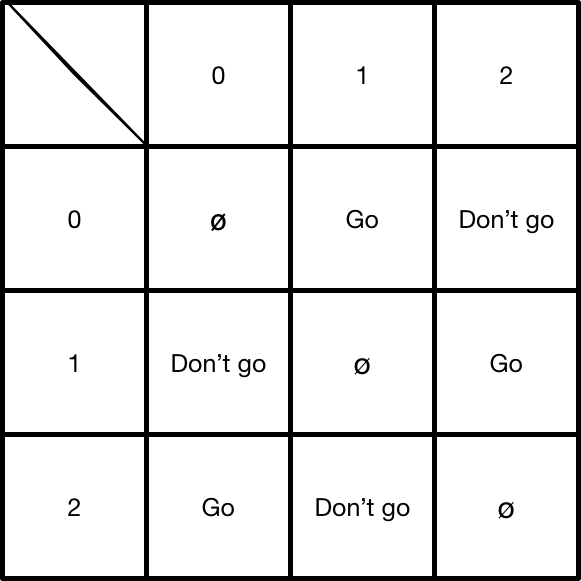
Instead of writing the distances, we will create a table telling wether we should or shouldn't go to a node based on the number of the current node.

This table should be complementary : if 0->1 means go, 1->0 means do not go. Because of that, we discard 0->0 , 1->1 and 2->2. Even tough we have 6 possibilites, it is possible to find a table that does what we want.

To mark each node with the correct integer, we start by doing a DFS from the root. We can choose any integer for the root, so we choose 0 . At each step, we write for the children of our current vertex the number such that it means “Don't go”.

Decoding is easy because of the table. The only case we need to be aware is for the root, because in that case we will find only “Don't go”, so we must return the own vertex in that case.

Subtasks 3 and 4 : 0 and 1

With only two numbers , it is impossible to find a table like the previous one. In order to solve the problem , we must try a different strategy or find some implicit information that we have not used so far.

In this case, we will go with the second option. At the current point, we have not taken advantage of the fact that the number of the vertices remain the same. That is a lot of information !

Our previous solution relied heavily on the idea of the complementary table. We need to find some information that is complementary and uses the number of the vertices.

An operator that does exactly that is the less than operator. If  (a < b) equals true, then (a > b) equals false. This was the implicit information we were looking for.

In order to decide wether we should or shouldn't go from vertex A to B, we will calculate the following value : v = (integer written on A) + (integer written on B) + (A < B). If v is an even number, then we do not go. If v is an odd number, then we go.

Because of the complementary nature of the less operator, if v means “Go” to A, then it will mean “Don't go” to B.

To mark the correct integer on each node, we start by doing a DFS from the root. For each children, we choose the correct integer such that we write “Don't go” from the current node.

Even tough there was a lot of thinking , the final code is very simple. Wow!