Divide and Conquer #4 - ICC

This is the fourth post of a series that focuses on Divide and Conquer. If you want to check the previous one, click here.

The problem we will analyze is ICC from the Central-European Olympiad in Informatics (CEOI 2016). You may find the problem statement here and a place to submit the solution here.

A synthesis of the problem statement is : there are N cities numbered from 1 to N. At each pass, we build a new road between two cities such that there is no cycle between them. You must guess the new road by asking the following question : is there an edge from a vertex of set A to a vertex of set B? The total number of queries for the N-1 passes must not exceed M queries. There are five subtasks with different (N,M) pairs, but N = 100 and M = 1625 for the last one.

The fact that the statement mentions roads and cities heavily suggests that this is a graph problem. Indeed, it is one!

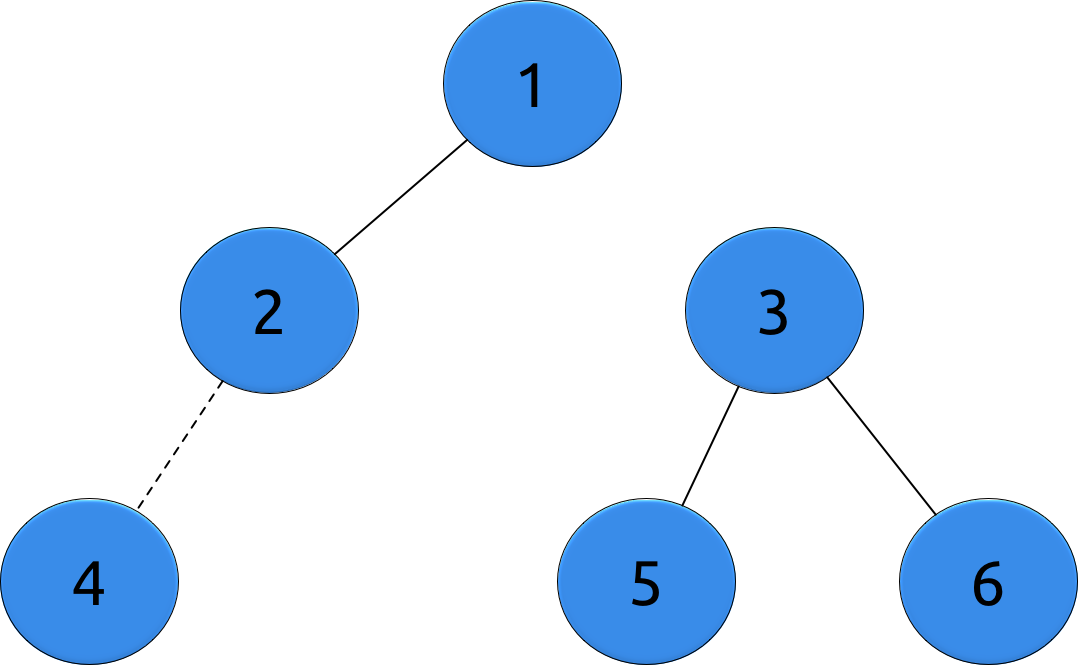
• Every city is a vertex
• Every road is an edge
• Our graph is a forest
• At each pass, we add an edge between vertices of different forests
• Just by modeling the problem with a graph we arrive at the most simple solution:

O(N^3) : 7 points

At each pass, we query all possible edges. Notice that the possible edges do not include edges that connect two vertices of the same forest because of the acyclic property of our graph. In order to maintain that, we use an Union-Find data structure.

To check wether or not there is an edge between two vertices, we do a query with unitary sets containing these vertices.

The complexity analysis is not complicated. There are O(N^2) edges and O(N) passes, so the total number of queries is O(N^3).

O(N^2) : 18 points

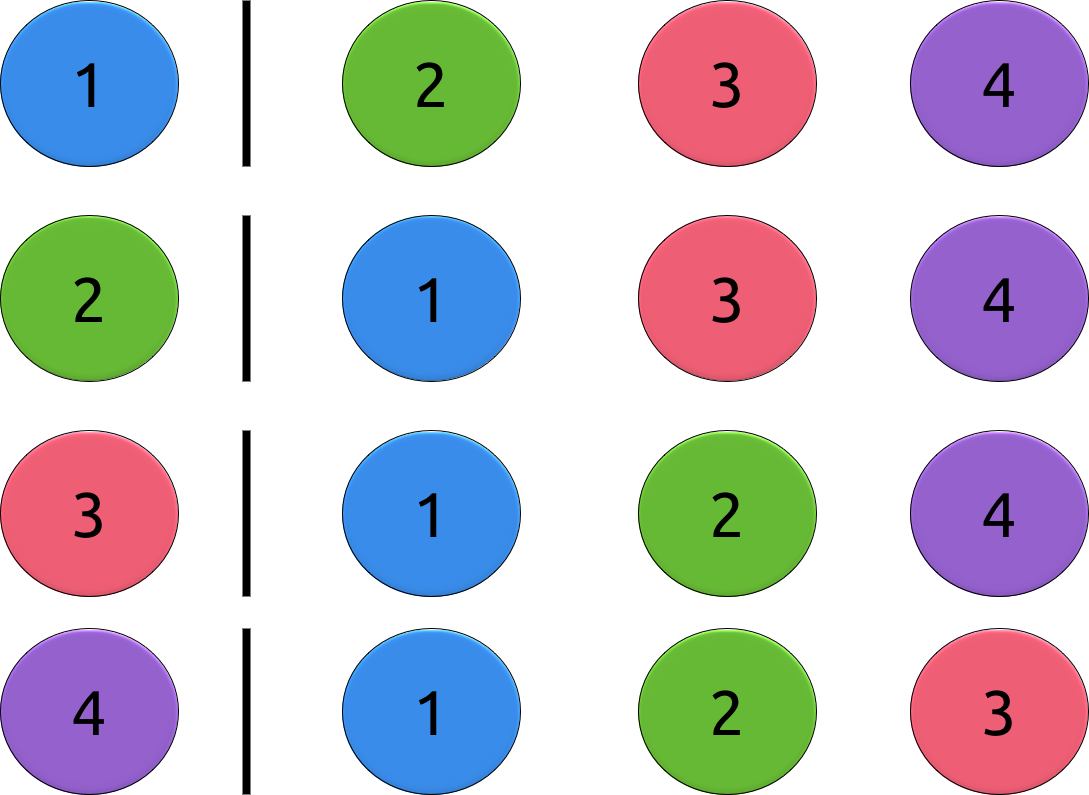
To reduce the number of queries, we will not try to discover directly the pair of vertices that is connected by the new edge. Instead, we will try to discover for each vertex if it is the one with a new edge.

To do that we do the following query : we put the vertex we are considering now in a unitary set and all the vertices that are not on the subtree of this vertex. The image above exemplifies this.

There will be two vertices that have new edges. These were the vertices we wanted to know and the new edge connect those vertices. The overall complexity is O(N) per pass and there are O(N) passes, so in total its O(N^2).

Room for improvement : the start of D&C

Suppose that we found the first vertex that has a new edge. We can use a Divide and Conquer algorithm to find the other one because we know it is on the set we have just asked about.

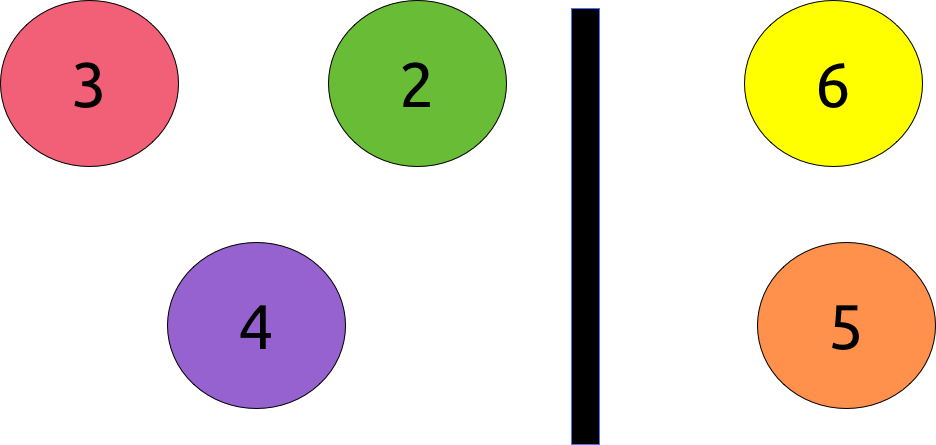
Let's exemplify the algorithm with an example. Suppose we discovered that the vertex 1 has the new edge and the other vertex is on the set {2,3,4,5,6}. We split the set into L = {2,3,4} and R = {5,6} and do the query with sets {1} and L. If there is an edge between 1 and L , then we can discard R because there is only one edge. Similarly, if there is not, we discard L and continue with R. We continue to do that until we end with a set with only one element : the last element is the other vertex of the edge.

So our “Divide” part is to split the set into two halves L and R and do the query between the known vertex and L. The “Conquer” part is to discard L or R based on the result of our query. The base case is the unitary set.

This improvement alone does not give any extra points. However, the idea of the final solution uses this improvement.

A desire : the perfect environment 

Suppose we had two sets A and B and we knew that there is a new edge from a vertex of set A to one on set B. If this happened , we could adapt the above algorithm to discover the two vertices very quickly.

If we fixed the set A for all the queries and did the above procedure on B, we would find the vertex that has the edge on B. We could also fix B and run the algorithm on A, discovering the vertex on A.

So the D&C part of the problem has ended. If we could find those two sets, the problem would be solved. But can we?

The answer is fortunately yes.

O(N*log(N) + N*K) : 61 points

The first idea two find the two sets is to use some randomization. Suppose that we put the connected components we have so far (represented by the head of the component) in a sequence and randomly shuffle the sequence. Then , we split the sequence into two halves. The probability that the components whose vertices form the new edge are on different halves if of 50%. We then construct two sets : A with the vertices of the components on the first half and B with the remaining ones. If there is an edge from A to B , we stop the shuffling and run the D&C algorithm. Otherwise, we continue until we arrive in a partition.

The number of passes algorithm is not defined. However, we could say that on average it will need K passes. A good estimative of K is a K that gives a probability close to 1 that the partition will be found. Because 1 - (0.5)**10 >= 99.9%, K = 10 seems to be a reasonable one.

The overall complexity is O(log(N) + K) per pass and therefore O(N*log(N) + N*K) total complexity.

O(N*log(N)) : 90 points

The final solutions uses a quicker approach to arrive at the partition.

The partition used is based on a simple principle with a clever application. The idea is : every number written in its binary form has at least one different bit if we compare it to another number.

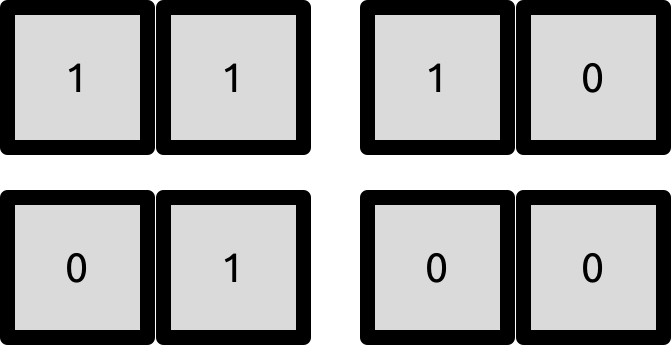
You may take a look at the image above with the representation of {0,1,2,3} in binary base and convince yourself. The formal proof is not that hard, but I will omit it.

Because of the principle above, the following strategy will find a partition : first, we assign a integer from 0 to C-1 for each component.

Then, for each bit, we separe the vertex into two sets A and B according to the state of that bit. A contains the vertices whose component number has the bit we are considering turned off and B contains the vertices whose component number has the bit turned on. We test this partition : if it works, then we run the D&C algorithm; if it does not, we follow to the next bit. By doing that, we achieve O(log(N)) to discover the partition which is a small improvement against the last algorithm, but scores more points because of the tight query limit.

O(N*log(N)) : 100 points

The solution mentioned above is 99% similar to the final solution. The only diference is that in order to achieve 100 points you need to do some micro optimizations.

The first idea to reduce the number of queries is to shuffle the order that you choose the bit to do the partition. The grader is adaptative and tries to achieve the worst case complexity if you always ask about the bits in order, so shuffling prevents this from happening. If you implement this idea alone you should score 100 points.

The second idea is to save a query per iteration when doing the partition. Imagine there are K bits to try the partition and you have tried K-1 of them. You do not need to check if the last one will find a valid partition, because it must. This is a small gain but helps.

My solution to this problem :