Divide and Conquer #3 - Library

This is the third post of a series that focuses on Divide and Conquer. If you want to check the previous one, click here.

The problem we will analyze is Library from the Japanese Olympiad in Informatics Spring Camp (JOI SC 2018). You may find the problem statement here and a place to submit here.

A synthesis of the problem statement is : you have an array of size N (N <= 1000) that is a permutation of 1,2,3… N. At the beginning you do not know the configuration of the array. However, you are allowed to make up to 20000 queries which count the number of subarrays of the subset of numbers you are querying. After that, you must output one of the two possible configurations of the array.

Our first step in order to solve the problem is to transform it into a graph problem:

• Every number of the array is a vertex
• There is an edge between every two adjacent numbers in the array
• Our query answers the number of connected components of the subgraph we chose for that query.

This first steps leads very quickly to the solution to subtask 1:

O(N^2) : 19 points

We simply try to discover all edges of the graph. To check wether or not there is an edge , we do a query with only two elements. If there is one connected component, then there is an edge. Otherwise, there is not an edge.

After that, you can do a BFS/DFS starting from one of the two vertices with degree one and find one of the two possible answers.

O(N*log(N)) : 100 points

We have about 20 queries per vertex in order to discover the configuration of the array. This heavily suggests around O(log(N)) queries per vertex, which is a hint that Divide and Conquer might work.

The first step of our algorithm will be adding the vertices in order :

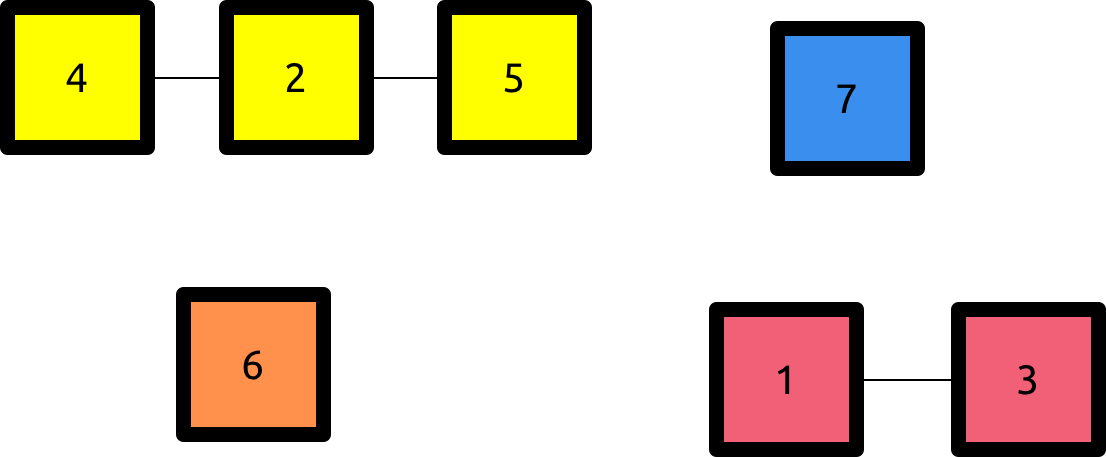
When we adding the i-th vertex, the other i-1 vertices form C  connected components. Each component has two endpoints (note that the endpoints can be equal when there is only one element). You may think of these components as floating subarrays whose order is still to be defined. In the image, there is an example for a situation where we are adding the vertex 8.

There are three possible cases for our newly added vertex :

• Zeroth case : there is no edge between i and the other components , therefore i is a part of a new connected component and the total number of components is increased.
• First case : there is exactly one edge of i to one of the endpoints of the components. The number of components remains the same.
• Second case : there are exactly two edges between i and two endpoints of different components. Therefore we merge two components in this step and the total number decreases by one.

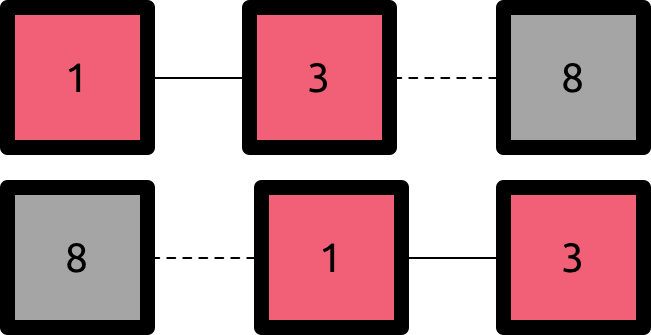
To make the last two cases clearer, you may look at the examples above of the first and second case , respectively.

The first query we will make for our new vertex is asking about the configuration with all the C  components and the vertex. The answer of the query uniquely determines the case : if there are C+1 components, then we know it is case 0 and we can continue our algorithm; if there are C components, then we know it is case 1 and we need to discover the component the i-th vertex is connecting and which vertex it is connecting to; the last option is that there are C - 1 components, in which we need to discover the two components and the two distinct endpoints.

The next step of our solution is to create a D&C algorithm for the first case. It turns out that this algorithm is very similar to the algorithm of our last two posts :

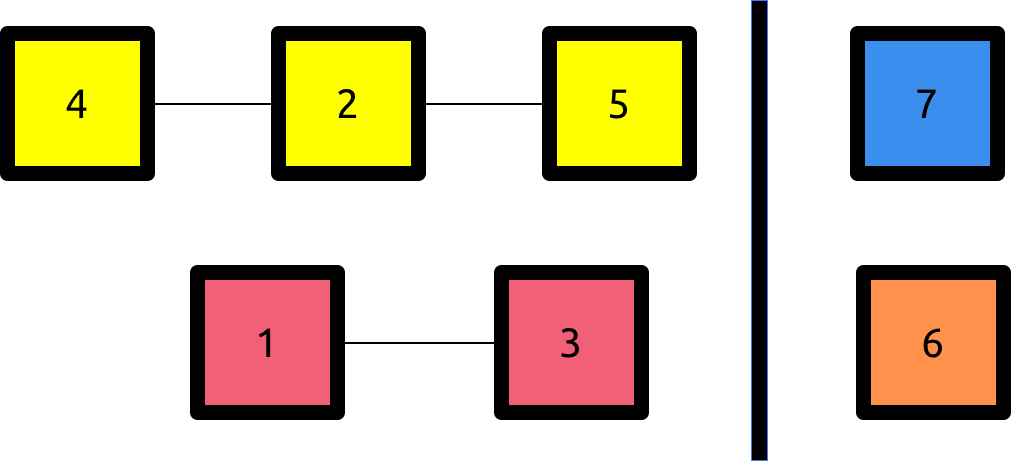
We split the set of the components we have into two halves, L and R. We then try a configuration with the components of L and the i-th vertex. If there are |L| + 1 components in that configuration, then there is no edge between the i-th vertex and the components of L and we discard all components of L , because we know that the edge is on R. Otherwise, the number of components is |L| and we discard all components of R because of the same concept.

Notice that when we do an iteration, we discard half of the components and arrive at the same problem we had before. If we continue to do that, we will eventually reach the case where there is only one component : this is our base case and the last component is the one we are looking for.

After that, we need to discover the vertex that connects with the i-th one. This is very simple and can be done with one query : try to check if there is an edge between the i-th vertex and one of the endpoints the same way we did in the previous solution. If there is one, then we found the edge. If there is not, then the edge will be between the other endpoint and the i-th vertex. After that, you must not forget to update the component you found and its endpoints.

The last step of our algorithm is to create a D&C algorithm for the second case. This part is a little bit more complicated compared to the last one, but not that much.

The “Divide” part of our algorithm is identical to the last one. We split the set we are querying into two sets L and R. The change is on the “Conquer” part, because now there are three possible results for our query with L plus i-th vertex.

• |L| - 1 components : the two edges are on L. We discard R and recurse into the same problem we had, that is , a set in case 2.
• |L| + 1 components : the two edges are on R. We discard L and recurse into the same problem we had.
• |L| components : there is one edge on L and consequently one on R. We recurse into two independent problems, which is to find exactly one edge in a set. This is the first case of our algorithm!

Therefore, the “Conquer” step may recurse into one problem of case 2 or two problems of case one. Our base case will be the same as case 1.

After we discovered the two components, we need to discover the vertices we connect to. We do exactly the same procedure as in case 1, but we need to be more careful when updating and merging the components.

A code that implements the idea and scores 100 points follows: