Divide and Conquer #1 - Carnival

This is the first post of a series of posts about Divide and Conquer. The idea is to share this simple yet very powerful approach to solve some problems.

This is by no means a complete tutorial about Divide and Conquer and I will assume that the reader is at least familiar to some of the key concepts of the technique and the well-known applications such as Merge Sort and Binary Search.

The problem we will analyze is Carnival from the Central-European Olympiad in Informatics (CEOI 2014). You may find the problem statement here and a place to submit the solution here.

After reading the problem statement it seems very smart to model it with a graph:

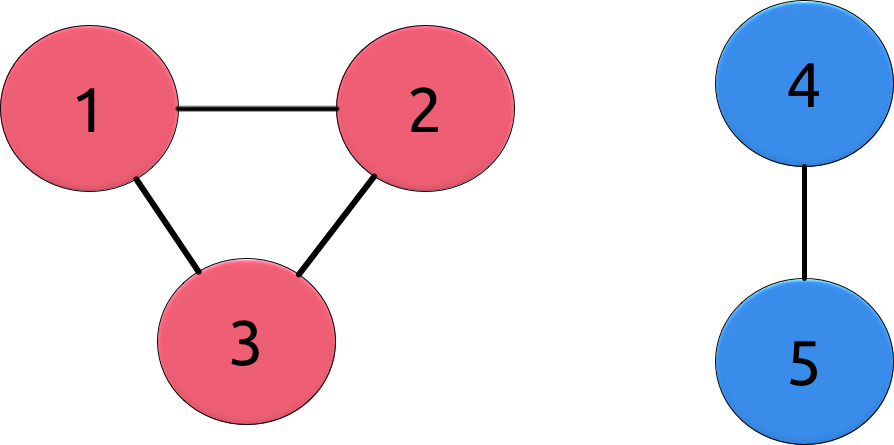
• Every person is represented as a vertex in our graph.
• Every costume is represented by a color in our graph. Each vertex has only one color.
• Every vertex is part of a connected component of vertex with the same color. This connected component is a clique.
• When we organize a party, we query the number of distinct colors of the set of vertices we chose.

Modeling the problem with the graph helps us arrive at the first partial solution:

O(N^2) queries : 20 points

A direct approach to solve the problem is to discover all the edges of the graph. To discover if there is an edge between two vertices, we organize a party with these two vertices. If there are two costumes, then they are of different colors and there is no edge. Otherwise, they share the same color and there is an edge between them.

Optimized O(N^2) : 100 points

There are some optimizations to make the previous solution work faster.

The first idea is to choose a head to each component we know so far and always ask questions with it . Because of the clique property, it does not matter which pair of vertices we query : any of them will  do the work. This saves lots of questions

The second idea is to add vertices gradually. We will first query 1, then 2, 3 and so on. This allow us to the following query : organize a party with the H heads we know so far and the i-th vertex we are adding. If in this party there are H + 1 costumes, then we know that the i-th vertex has no edge to any of those heads and is therefore a head of its own component. In the other case there will be H costumes and we need to query all the possible edges to discover the component of the i-th vertex.

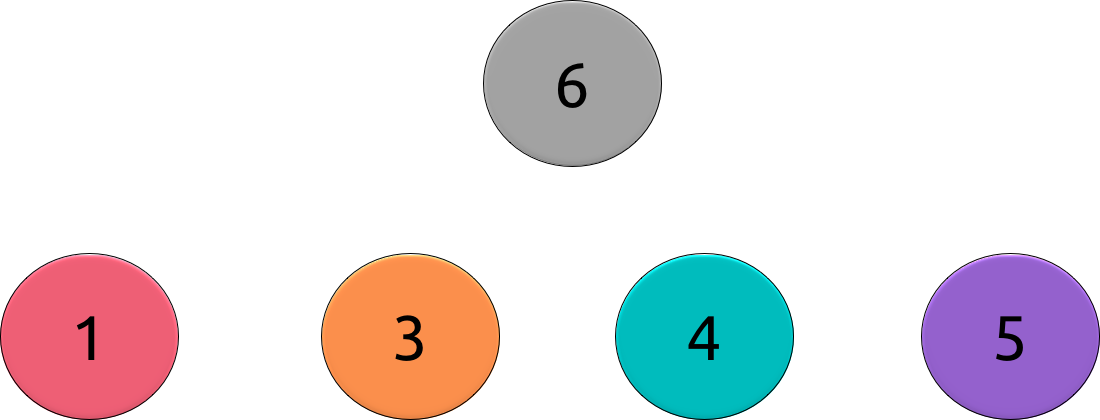
To make it clearer , see this example : we are adding vertex 6 and we know there are 4 head nodes : 1,3,4,5. If we organize the party and there are 5 costumes, then vertex 6 must have a color different from the other 4 vertices. In the other case, with 4 costumes, 6 must have the same color of one of those vertices. In that case, we find the color of 6 by testing an edge with each head.

The number of queries is still quadratic because of the case were the i-th vertex is not a new head. However, the constant is heavily reduced. This probably was not the intended solution, but it works.

O(N*sqrt(N)) : 100 points

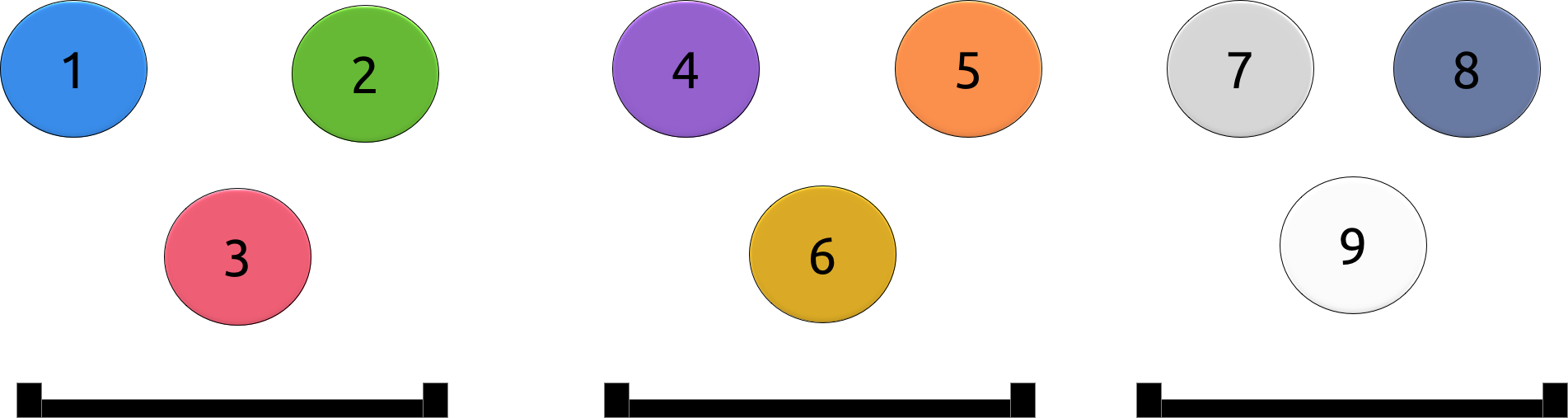
An idea to optimize the previous solution is to group the heads into buckets. We do the first query with all the H heads to discover wether the i-th vertex is a new head or not in the same way as before.

But the second part changes. Instead of manually testing all edges with the heads, we group them into B buckets with H/B per bucket. Then we organized parties with the i-th vertex and all heads of each bucket. If there are H/B + 1 costumes, then we proceed to the next bucket. Otherwise, we test the edge with all the heads of this bucket.

This gives B + H/B queries per vertex. The value of the that minimizes this sum is sqrt(H). Therefore we achieve the complexity of O(N*sqrt(N)), better than the last one.

O(N*log(N)) : 100 points

The title of this post includes “Divide and Conquer” and so far none of the solutions used it, so at some moment D&C must appear. This is the moment!

The principle we will use is the same from the previous solutions. However, we will use it way more efficiently.  The idea of querying H heads plus the i-th vertex and deciding wether or not there is a edge based on the answer will be our base.

To start, we do the now usual query with all heads like in the previous solution.

If there is an edge, then we start to use D&C. The “Divide” part of our algorithm will be to partition our set of heads in two halves, L and R and querying the heads of L and the i-th vertex.

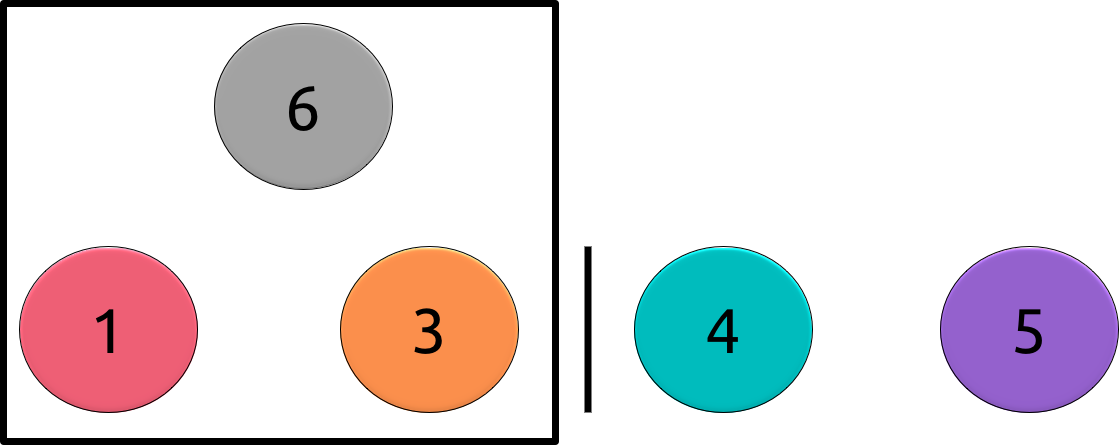
The “Conquer” part of our algorithm is based on the result of our query and the fact that there is only one edge between the i-th vertex and the whole set. If that edge is on the set L, then we can discard all the heads of R. If that edge is not on that set, then it must be on R,because there is exactly one edge so we discard all heads of L.

Let's make another example with adding 6 , knowing heads 1,3,4,5. We split the heads in {1,3} and {4,5} and do the query {1,3,6}. Suppose we received that there are 3 colors in the set. Then there is no edge between 6 and {1,3} and we now solve the problem with the set {4,5}.

If we continue to do the procedure of discarding a half in each iteration, we will eventually reach our base case : the set has only one element. Therefore , there must be an edge between the i-th vertex and the last element.

If we want to analyze the complexity , we must think about the depth of the recursion we designed. In each iteration, we discard H/2 heads so the depth will be at most log2(H). Thus the overall number of queries is O(N*log(N)).

My implementation of this idea: